Come leggere un disegno in scala? Se non sapete come risalire alle misure reali di una pianta o di un prospetto, ecco qui un breve tutorial con alcuni esempi pratici.
Che cos’è una scala?
Prima di entrare nell’argomento, capiamo bene che cos’è effettivamente una scala. Intendiamo per “scala” quel metodo di rappresentazione mediante il quale, riportiamo su di un foglio, il disegno di un oggetto esistente nella realtà. Esistono scale di riduzione e scale di ingrandimento.
Nelle scale di riduzione, che si utilizzano nell’edilizia e nel design, il foglio è generalmente molto più piccolo rispetto, ad esempio, ad una casa reale. Per questo quella casa, deve essere ragionevolmente ridotta nelle sue proporzioni, in maniera tale da poter rientrare nello stesso foglio. La scala che noi utilizziamo dunque, non fa altro che dividere una certa misura reale per un numero o fattore.
Esempi di Scale di Riduzione
Come già detto, le scale di riduzione si usano nell’edilizia, nell’urbanistica, ma anche nell’arredamento. E in generale, in tutti quei casi in cui l’oggetto da rappresentare (una casa, un lotto di terreno, un mobile) è più grande del foglio. Di seguito alcuni esempi di scale di riduzione nei quali illustriamo quanto misurano sul foglio 10 metri nelle varie scale.
Esempio A)
Per la scala 1:100 si ha: 10 metri (misurati nella realtà), divisi per il numero 100, corrispondono sul foglio a 0,1 metri (cioè a 10 centimetri).
SCALA 1:100
10 mt reali / 100 = 0,1 mt sul foglio (= 10 cm)
Esempio B)
Per la scala 1:50 si ha: 10 metri (misurati nella realtà), divisi per il numero 50, corrispondono sul foglio a 0,2 metri (cioè a 20 centimetri).
SCALA 1:50
10 mt reali / 50 = 0,2 mt sul foglio (= 20 cm)
Esempio C)
Per la scala 1:20 si ha: 10 metri (misurati nella realtà), divisi per il numero 20, corrispondono sul foglio a 0,5 metri (cioè a 50 centimetri).
SCALA 1:20
10 mt reali / 20 = 0,5 mt sul foglio (= 50 cm)
Esempio D)
Per la scala 1:200 si ha: 10 metri (misurati nella realtà), divisi per il numero 200, corrispondono sul foglio a 0,05 metri (cioè a 5 centimetri).
SCALA 1:200
10 mt reali / 200 = 0,05 mt sul foglio (= 5 cm)
Esempio E)
Per la scala 1:1000 si ha: 10 metri (misurati nella realtà), divisi per il numero 1000, corrispondono sul foglio a 0,01 metri (cioè a 1 centimetro).
SCALA 1:1000
10 mt reali / 1000 = 0,01 mt sul foglio (= 1 cm)
Esempi di Scale di Ingrandimento
Le scale di ingrandimento si usano molto in meccanica, nel design, e in generale in tutti quei casi dove gli oggetti da rappresentare sono molto piccoli. Il criterio che si utilizza nella rappresentazione cambia un pò, anche se in sostanza rimane lo stesso. Dobbiamo cioè fare un discorso non più di divisione ma di moltiplicazione, moltiplicando tutte le misure per il fattore della scala. In questo caso il fattore, o valore della scala, viene prima dei due punti: in un rapporto 5:1, il valore è dunque 5.
Esempio F)
Per la scala 2:1 si ha: 1 centimetro (misurato nella realtà), moltiplicato per il numero 2, corrisponde sul foglio a 2 centimetri.
SCALA 2:1
1 cm reale x 2 = 2 cm sul foglio
Esempio G)
Per la scala 10:1 si ha: 1 centimetro (misurato nella realtà), moltiplicato per il numero 10, corrisponde sul foglio a 10 centimetri.
SCALA 10:1
1 cm reale x 10 = 10 cm sul foglio
Il disegno è in scala?
Prima di procedere con la lettura delle misure, dovete innanzitutto capire se il disegno che avete di fronte è veramente in scala. I disegni che sono stati scansionati, solitamente, non lo sono.
Questo perché in fase di acquisizione dell’immagine, si impostano dei parametri digitali (i dpi, ovvero, i pixel/pollice) che possono modificare le dimensioni del foglio che state acquisendo e quindi anche la scala.
Generalmente i disegni che conservano la scala sono quelli contenuti in files PDF. Questo perché un file PDF viene solitamente generato da un tecnico (architetto, ingegnere, geometra) mediante un software CAD con cui viene impostata la scala di rappresentazione. Ovviamente ci si deve accertare però che lo stesso file non abbia subito manipolazioni successive. A tal proposito, abbiamo già parlato in un articolo specifico, di come acquisire e stampare correttamente un disegno in scala.
Misuriamo il nostro disegno in scala
Ora che ci siamo accertati di avere effettivamente un disegno in scala, dobbiamo procurarci uno strumento utile per la sua lettura. Prendete quindi un righello, o una squadretta, o un qualsiasi oggetto che sia graduato in centimetri. Apponete il righello in prossimità di una linea del disegno e leggete i centimetri di tale linea. Ipotizziamo, ad esempio, che abbiamo rilevato 11 centimetri.
Adesso facciamo caso al valore della scala: nel disegno dovrebbe essere segnato in un margine del foglio. Sottolineiamo che il valore della scala (ipotizziamo sia 1:50), è un numero puro, cioè un numero adimensionale, che non ha alcun indice di misura.
Ecco i dati
del mio problema:
– misura rilevata con la squadretta = 11 cm
– valore della scala = 50
per risalire
alla misura reale del segmento che ho misurato non devo fare altro che una
semplice moltiplicazione:
misura squadretta x valore scala = misura reale
in numeri:
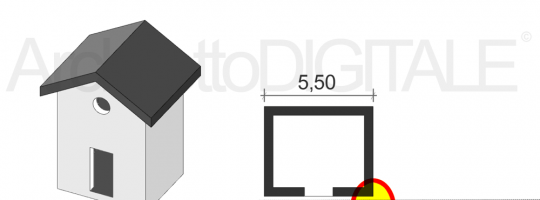
11 cm x 50 = 550 cm (che corrispondono a 5,50 m)
Il segmento che ho misurato sul foglio di 11 centimetri corrispondono dunque, in scala 1:50, a 5,50 metri.
Conclusioni
Abbiamo visto come leggere correttamente un disegno in scala. Ricorda: assicurati sempre che il tuo disegno sia davvero in scala prima di iniziare a convertire le misure. Buon Lavoro!